Exercises
6. Using the polar coordinate, we denote the distance between to point inside the sphere is $$s=\int\sqrt{dr^2+r^2d\theta^2}=\sqrt{r'(\theta)^2+r(\theta)^2}d\theta,$$and the velocity at any $r$ satisfy, in which $k=\dfrac{2GM}{R^3},$ $$kr_0^2=v^2+kr^2\,\implies\, v=\sqrt{k(r_0^2-r^2)}.$$ Therefore the time between the two points is $$t=\int{\sqrt{\frac{r’^2+r^2}{k(r_0^2-r^2)}}d\theta}.$$ Thus we can take the Lagrangian as $\mathcal{L}=\sqrt{\dfrac{r’^2+r^2}{r_0^2-r^2}}$, then the Hamiltonian is $\mathcal{H}=r’\dfrac{\partial\mathcal{L}}{\partial r’}-\mathcal{L}=-\dfrac{r^2}{\sqrt{r_0^2-r^2}\sqrt{r’^2+r^2}}.$ Since the Lagrangian doesn’t contain $\theta$ explicitly, the Hamiltonian is conserved. $$-\dfrac{r^2}{\sqrt{r_0^2-r^2}\sqrt{r’^2+r^2}}=h$$ $$\implies d\theta=\frac{dr}{\sqrt{\frac{r^4}{h^2(r_0^2-r^2)}-r^2}}.$$ When $r=\sqrt{\dfrac{h^2}{h^2+1}}r_0$, the denominator is $0$, we measure $\theta$ from this point. Doing this integral, we have, $$\theta=\arctan{\sqrt{\frac{r^2}{h^2(r_0^2-r^2)}-1}}-\sqrt{\frac{h^2}{h^2+1}}\arctan{\sqrt{\frac{r^2}{(h^2+1)(r_0^2-r^2)}-\frac{h^2}{h^2+1}}}.$$ When $r=r_0,\, \theta_c=\dfrac{\pi}{2}\left(1-\sqrt{\dfrac{h^2}{h^2+1}}\right)$. This is the equation of hypocycloid. Then the time for traveling between the two point is $$t=-2\int_0^{\frac{r_0^2}{h^2+1}} \frac{d(r_0^2-r^2)}{2\sqrt{k}\sqrt{\left[r_0^2-(r_0^2-r^2)\right](r_0^2-r^2)-h^2 (r_0^2-r^2)}}=\frac{\pi}{\sqrt{k}\sqrt{1+h^2}}.$$ When the two points are on the surface of the Earth, denoting the distance as $s$. Then in the above equation, $r_0=R,\,h=\dfrac{\pi R-s}{\sqrt{(2\pi R-s)s}},$ then, $$t=\sqrt{\frac{(2\pi R-s)sR}{GM}}$$ For the Earth, $R\approx6371\text{km},\,G\approx6.67\times10^{-11}\text{N}\cdot\text{m}^2/\text{kg}^2,\,M\approx5.965\times10^{24}\text{kg}.$ From New York to Los Angeles, $s\approx 4800\text{km}$, thus it takes, $$t\approx1645.1\text{s}.$$ And $h\approx1.17$, then, $$r_{min}\approx4843.1\text{km}$$
15. Considering a Wheatstone bridge as the figure,
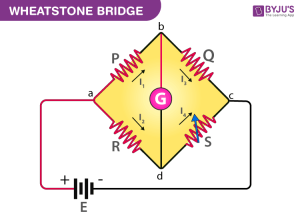
put a inductance L on P and a capacitance C on S. Taking four generalized coordinate as $q_i,\, i=1,2,3,4$, and $q$. Then we have the Lagrangian, $$\mathcal{L}=\frac{1}{2}L\dot{q_1}^2-\frac{q_4^2}{2C}+E(q_1+q_2),$$ the dissipation function $$\mathcal{F}=\sum_{i=1}^4\frac{1}{2}R_i\dot{q_i}^2,$$ and the constraint by the Kirchhoff junction conditions, $$f_1=\dot{q}-\dot{q_1}-\dot{q_2}=0,$$ $$f_2=\dot{q}-\dot{q_3}-\dot{q_4}=0,$$ Therefore the Lagrange equation of motion, $$\frac{d}{dt}\frac{\partial \left(\mathcal{L}+\lambda_1 f_1+\lambda_2 f_2\right)}{\partial \dot{q_i}}-\frac{\partial\left( \mathcal{L}+\lambda_1 f_1+\lambda_2 f_2\right)}{\partial q_i}+\frac{\partial \mathcal{F}}{\partial \dot{q_i}}=0.$$ \begin{align}\implies \begin{cases} L\ddot{q_1}-\dot{\lambda_1}-E+R_1\dot{q_1}=0,\\ -\dot{\lambda_1}-E+R_2\dot{q_2}=0,\\ -\dot{\lambda_2}+R_3\dot{q_3}=0,\\ -\dot{\lambda_2}+\dfrac{q_4}{C}+R_4\dot{q_4}=0,\\ \dot{\lambda_1}+\dot{\lambda_2}=0.\end{cases}\end{align} By eliminating the $\lambda$’s we can reduce to, \begin{align}\begin{cases}L\ddot{q_1}-R_2\dot{q_2}+R_1\dot{q_1}=0,\\-R_3\dot{q_3}+\dfrac{q_4}{C}+R_4\dot{q_4}=0,\\L\ddot{q_1}-R_3\dot{q_3}-E+R_1\dot{q_1}=0.\end{cases}\end{align} These are the usual Kirchhoff loop equations.
22. The Lagrangian of the particle is $$\mathcal{L}=\frac{1}{2}m\mathbf{\dot{r}}^2-V(\mathbf{r})+\lambda\sigma(\mathbf{r},t)$$ Because the Hamiltonian is $$\mathcal{H}=\mathbf{\dot{r}}\frac{\partial \mathbf{\mathcal{L}}}{\partial{\mathbf{\dot{r}}}}-\mathcal{L}.$$ Therefore $$\frac{d\mathcal{H}}{dt}=-\frac{\partial \mathcal{L}}{\partial t}.$$ Because of the explicit dependence of $t$ of $\sigma(\mathbf{r},t)$, the Lagrangian is a function of t explicitly. Then the Hamiltonian (which is the energy) is not conserved. The physical reason of the nonconservation of energy is that the constrain force due to the surface does work.
23.
(a) Denote position of $m_1$ as $(r_1,\theta_1,z_1)$, position of $m_2$ as $(r_2,\theta_2,z_2).$ Then the Lagrangian is \begin{align}\mathcal{L}=&\frac{1}{2}m_1(\dot{r_1}^2+r_1^2\dot{\theta_1}^2+\dot{z_1}^2)+\frac{1}{2}m_2(\dot{r_2}^2+r_2^2\dot{\theta_2}^2+\dot{z_2}^2)-m_2gz_2\\&-\frac{1}{2}k\left[(r_1\cos{\theta_1}-r_2\cos{\theta_2)^2+(r_1\sin{\theta_1}-r_2\sin{\theta_2})^2+(z_1-z_2)^2}\right]\end{align}
(b) There are 4 constraints, \begin{align}\begin{cases}f_1=r_2-b=0,\\f_2=z_2-c=0,\\f_3=r_1-a=0,\\f_4=z_1=0.\end{cases}\end{align} The Lagrange equation of motion is \begin{align}&\frac{d}{dt}\frac{\partial \left(\mathcal{L}+\lambda_1 (r_2-b)+\lambda_2 (z_2-c)+\lambda_3 (r_1-a)+\lambda_4 z_1 \right)}{\partial \dot{q_i}}\\&-\frac{\partial\left( \mathcal{L}+\lambda_1 (r_2-b)+\lambda_2 (z_2-c)+\lambda_3 (r_1-a)+\lambda_4 z_1 \right)}{\partial q_i}=0.\end{align}\begin{align}\implies\begin{cases}\ddot{r_1}-r_1\dot{\theta_1}^2+\dfrac{k}{m_1}\left[r_1-r_2\cos{(\theta_2-\theta_1)}\right]-\lambda_3=0,\\ \ddot{r_2}-r_2\dot{\theta_2}^2+\dfrac{k}{m_2}\left[r_2-r_1\cos{(\theta_2-\theta_1)}\right]-\lambda_1=0,\\ \ddot{z_1}+\dfrac{k}{m_1}(z_1-z_2)-\lambda_4=0,\\ \ddot{z_2}-\dfrac{k}{m_2}(z_1-z_2)+m_2g-\lambda_2=0,\\r_1^2\ddot{\theta_1}+\dfrac{k}{m_1}r_1r_2\sin{(\theta_1-\theta_2)}=0,\\r_2^2\ddot{\theta_2}+\dfrac{k}{m_2}r_1r_2\sin{(\theta_2-\theta_1)}=0.\end{cases}\end{align} Using the constraints, we obtain that, \begin{align}\begin{cases}-a\dot{\theta_1}^2+\dfrac{k}{m_1}\left[a-b\cos{(\theta_2-\theta_1)}\right]-\lambda_3=0,\\-b\dot{\theta_2}^2+\dfrac{k}{m_2}\left[b-a\cos{(\theta_2-\theta_1)}\right]-\lambda_1=0,\\\lambda_4=\dfrac{k}{m_1}c,\\\lambda_2=m_2g-\dfrac{k}{m_2}c,\\\ddot{\theta_1}+\dfrac{kb}{m_1 a}\sin{(\theta_1-\theta_2)}=0,\\\ddot{\theta_2}-\dfrac{ka}{m_2 b}\sin{(\theta_1-\theta_2)}=0.\end{cases}\end{align} By the last two equations, we can obtain that, $$\ddot{\theta_1}-\ddot{\theta_2}=-\frac{k(m_2 b^2-m_1 a^2)}{m_1m_2 a b}\sin{(\theta_1-\theta_2)}$$ Assume that $\theta_1(0)=\theta_0,\, \theta_2(0)=0,\, \dot{\theta_1}=\dot{\theta_2}=0$, then we can do one integral, $$(\dot{\theta_1}-\dot{\theta_2})^2=\frac{2k(m_2 b^2-m_1 a^2)}{m_1m_2 b}\cos\left[{(\theta_1-\theta_2)-\theta_0}\right].$$ As we can see, $m\lambda_4$ and $m\lambda_2$ are vertical constrain force of $m_1$ and $m_2$ respectively, and $m\lambda_3$ and $m\lambda_1$ are horizontal constrain force of $m_1$ and $m_2$ respectively.
25. Take the position of the center of the disk $(x,y)$ and the angle it rotates $\phi$ as generalized coordinates. Denote the tangent point between the disk and the parabola as $(x_0,y_0)$. They satisfy, \begin{align}\begin{cases}x=x_0-\dfrac{2aR}{\sqrt{4a^2+1}},\\y=y_0+\dfrac{R}{\sqrt{4a^2+1}}.\end{cases}\end{align} Therefore the constraints, \begin{align}\begin{cases}f_1=y-\dfrac{R}{\sqrt{4a^2+1}}-a(x-\dfrac{2aR}{\sqrt{4a^2+1}})^2=0,\\f_2=R\dot{\phi}-\sqrt{\dot{x}^2+\dot{y}^2}=0\quad(\text{no slipping}).\end{cases}\end{align} Because the smallest radius of curvature of the parabola is $\dfrac{1}{2a}$, the condition of touching one point is $$R\le\frac{1}{2a}.$$
